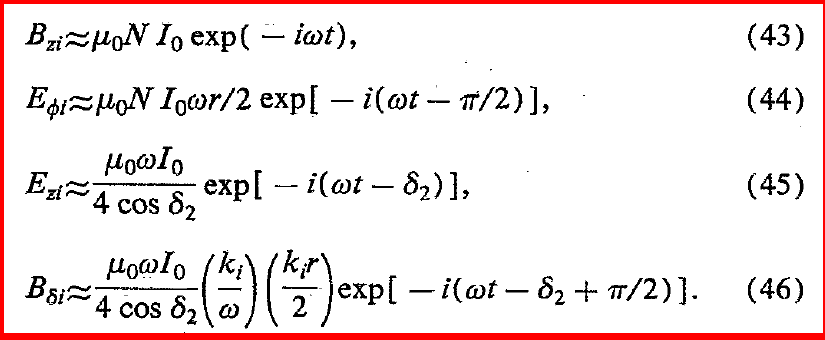6.3. Radiated Fields

Islam introduced a solution for retarded vector potential of a permeable infinitely-long cylinder loaded circular loop that is derived from Maxwell’s equations. Islam also noted that vector potential of a loop antenna that wrapped around the finite cylinder core is very difficult due to the complexity at the end of the cylinder. Resulting vector potential consisted of two parts: first part of potential was from loop alone and the other part was from the permeable core [31].

Islam then investigated methods of obtaining the electromagnetic field quantities (magnetic vector potential) due to a circular loop of current surrounding a prolate spheroidal core. First, static case was handled and then time-varying case was discussed [32].

#The field generated by J in the presence of core is the same as the superposition of the fields generated in the absence of the core by J and the volume density of magnetic dipoles (or currents) jω(μ-μ_0)H, where H is the magnetic field generated by J in the presence of the core and mu and mu0 are the permeabilities of the core and free space respectively [Rumsey and Weeks, 1956].

#Harmon investigated electric and magnetic fields of an empty solenoid at frequency up to 100 MHz. Inside and outside the solenoid are separated. The expressions for the field components are simplified if the frequency is less than 100 Mhz [Harmon, 1991].